This Science News Wire page contains a press release issued by an organization and is provided to you "as is" with little or no review from Science X staff.

Modeling the measurement precision of Fringe Projection Profilometry

November 7th, 2023
Modeling the measurement precision of Fringe Projection Profilometry
The full-chain noise models of the FPP system. Credit: Shenzhen Lv and Qian Kemao

Three-dimensional (3D) surface geometry provides essential information in various sciences and precision engineering. Fringe Projection Profilometry (FPP) is one of the most powerful non-contact (thus non-destructive) and non-interferometric (thus less restrictive) 3D measurement techniques, featuring at its high precision. However, the measurement precision of FPP is currently evaluated experimentally, lacking a complete theoretical model for guidance.

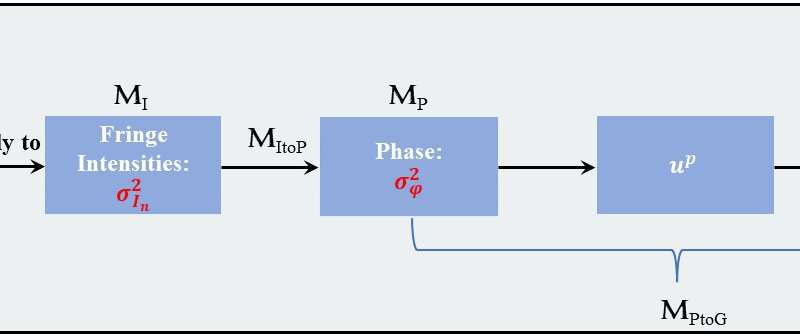
In a new paper published in Light: Science & Applications, a team of scientists, led by Professor Qian Kemao from School of Computer Science and Engineering, Nanyang Technological University, Singapore, and co-workers have proposed a complete and generic noise model chain with the following four stage models and two transfer models:

  • (S1) a model of camera noise (MC)
  • (S2) a model of fringe intensity noise (MI) by applying MC to fringe patterns
  • (S3) a model of phase noise (MP) which is important to evaluate the phase quality
  • (S4) a model of geometry noise (MG) which is important to evaluate the final geometry quality
  • (T1) a model to transfer noise from fringe intensity to phase (MItoP)
  • (T2) a model to transfer noise from phase to the geometry (MPtoG)

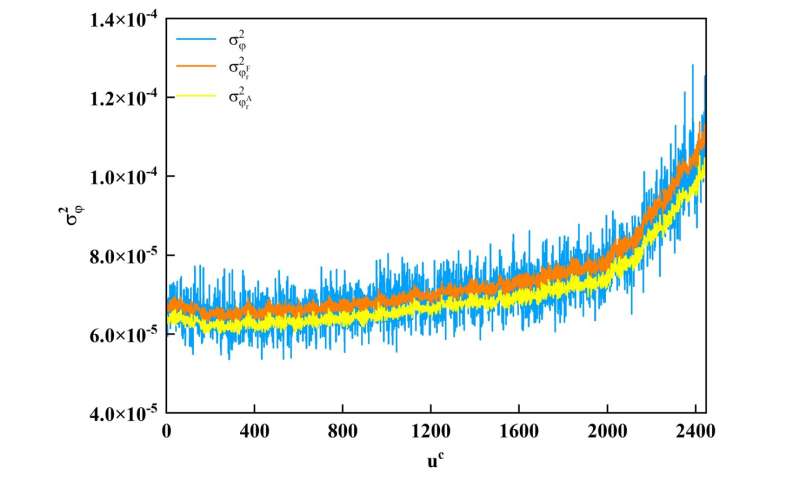
The first significant contribution of this work is the adoption of a non-Gaussian camera noise model, which, for the first time, establishes the connection between camera's electronics parameters (known in advance from the camera manufacturer) and the three phase precision models developed to enable to rapid estimation and comparison of the measured phases. An illustration presents the experimental validation results of the phase model, where the horizontal axis represents pixels, and the vertical axis represents phase variance. As observed from the graph, predictions from the full model (orange) and the approximate model (yellow) align closely with the measured data (blue).

Modeling the measurement precision of Fringe Projection Profilometry
Comparison between experiment results and theoretical phase models. Credit: Shenzhen Lv and Qian Kemao

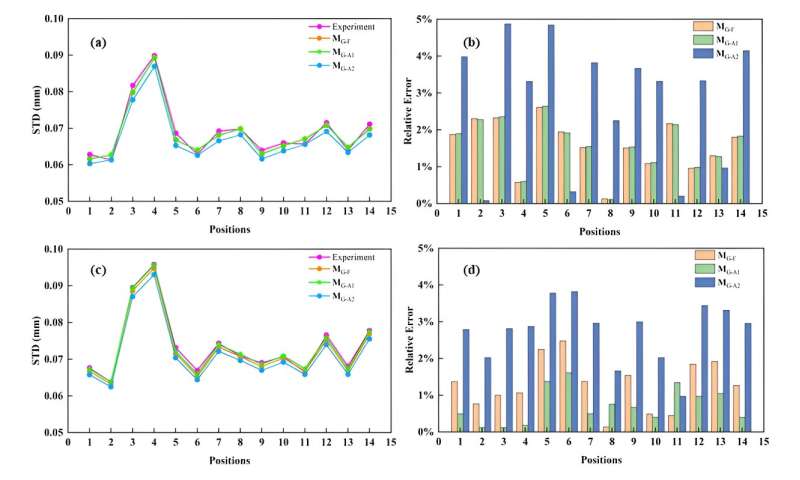
Another contribution of this work provides several measurement precision models by integrating the FPP system structure. These models include the full model MG-F, two approximate models MG-A1 and MG-A2, serving different purposes, and the precision limit model MG-L. An illustration presents the experimental validation results of the precision models in different regions of the camera, with relative errors all within 5%.

Modeling the measurement precision of Fringe Projection Profilometry
a, b the STD distributions and the relative error of the four methods at center ROI. c, d, the STD distributions and the relative error of the four methods at corner ROI. Credit: Shenzhen Lv and Qian Kemao

As a result, we not only establish the full precision model of the 3D geometry to characterize the performance of an FPP system that has already been set up, but also explore the expression of the highest possible precision limit to guide the error distribution of an FPP system that is yet to build.

Our theoretical models make FPP a more designable technique to meet the challenges from various measurement demands concerning different object sizes from macro to micro and requiring different measurement precision from a few millimeters to a few micrometers.

More information:
Shenzhen Lv et al, Modeling the measurement precision of Fringe Projection Profilometry, Light: Science & Applications (2023). DOI: 10.1038/s41377-023-01294-0

Provided by Chinese Academy of Sciences

Citation: Modeling the measurement precision of Fringe Projection Profilometry (2023, November 7) retrieved 29 April 2024 from https://sciencex.com/wire-news/460814561/modeling-the-measurement-precision-of-fringe-projection-profilom.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no part may be reproduced without the written permission. The content is provided for information purposes only.
Back to list