Einstein's missed opportunity to rid us of 'spooky actions at a distance'
Why do moving rulers shrink (length contraction) and moving clocks run slow (time dilation) such that everyone measures the same speed of light c, regardless of their relative motions? Einstein resolved this mystery at the turn of the 20th century in "principle fashion" by turning the question on its head. He invoked the relativity principle (AKA "no preferred reference frame") and argued that since c appears in the equations of physics, no preferred reference frame says that everyone must measure the same value for c regardless of their motions relative to the source (that is, regardless of their reference frames).
Length contraction and time dilation then follow as a result of this "light postulate." Ironically, he missed a chance to use the exact same principle to resolve the mystery of quantum entanglement, which he introduced in 1935, calling it "spooky actions at a distance." Indeed, he died believing that quantum entanglement was evidence that quantum mechanics was "incomplete" when his relativity principle would have told him that quantum mechanics is as complete as possible with respect to quantum entanglement.
Mystery No. 1
At the turn of the 20th century, physicists were trying answer the question: Why does everyone measure the same speed of light regardless of their motion relative to the source? This might not strike you as odd, but stop and think about it.
Suppose you and I are standing on a baseball field and I throw a ball as hard as I can to you at, say, 40 miles per hour. The ball moves away from me at 40 miles per hour and, since you are at rest with respect to me, the ball is moving toward you at 40 miles per hour. Now, suppose I ride on a golf cart moving toward you at 20 miles per hour and then throw the ball as hard as I can to you. The ball moves away from me and the golf cart at 40 miles per hour, which means the ball is moving toward you at 40 + 20 = 60 miles per hour. Makes sense, right?
But now suppose I use a flashlight and send light pulses toward you in both of those circumstances. In both cases, the light pulses move away from me at the speed of light c. So, do the light pulses approach you at c + 20 miles per hour when I'm on the golf cart? No, in both cases, you measure the light pulses to be moving toward you at c. How can that happen? That's the mystery they were trying to solve.
Physicists had a mathematical formalism (Lorentz transformations) whereby moving rulers shrank (length contraction) and moving clocks ran slow (time dilation) in such a way that everyone would then measure the same speed of light c. This movement of rulers and clocks would be relative to a substance that filled all of space called the "luminiferous ether." The problem was, the ether would need unheard of mechanical properties. For example, it would need a tensile strength greater than the hardest steel and yet allow the planets to move through it as if it weren't there at all. Enter Einstein.
Einstein's "principle resolution" of the mystery
Rather than try to explain length contraction and time dilation with respect to some hidden, preferred mechanical frame of reference, Einstein simply invoked the relativity principle. That is, if there are no preferred reference frames (AKA the relativity principle), then everyone must measure the same value for the speed of light c (a universal constant), regardless of their motions relative to the source (regardless of their reference frames). Length contraction and time dilation then follow from this "light postulate," i.e., the relativity principle applied to c. About this move, he said:
"By and by, I despaired of the possibility of discovering the true laws by means of constructive efforts based on known facts. The longer and the more despairingly I tried, the more I came to the conviction that only the discovery of a universal formal principle could lead us to assured results."
One-hundred fifteen years later, we are still using his theory of special relativity without any corresponding causal mechanisms ("constructive efforts") to account for its "universal formal principle," i.e., the relativity principle. That special relativity is a "principle theory" rather than a "constructive theory" is something not widely appreciated. Ironically, Einstein could have used this same relativity principle to resolve the mystery of quantum entanglement that he helped introduce in 1935.
Mystery No. 2
Nearly 40 years ago, David Mermin published a paper that Richard Feynman called, "One of the most beautiful papers in physics that I know." In "Bringing Home the Atomic World: Quantum Mysteries for Anybody," Mermin introduced his simple "device" that conveys the mystery of quantum entanglement to the general reader. The mystery of Mermin's device, and therefore quantum entanglement, is indeed easy to understand.
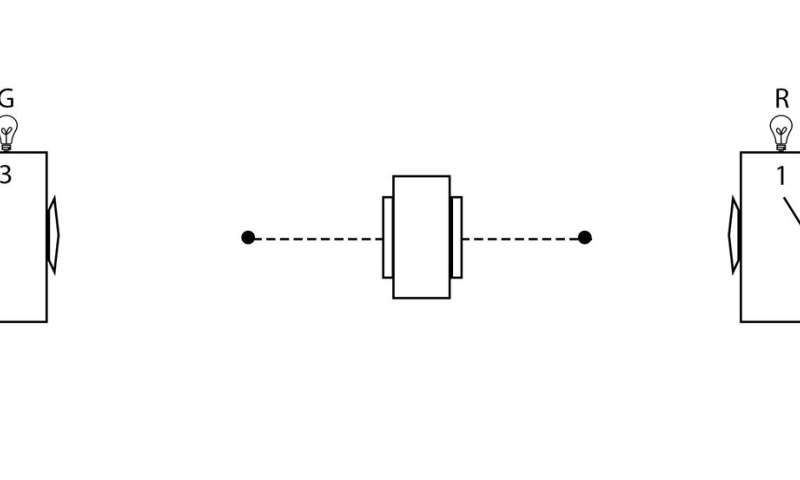
The Mermin device contains a source (middle box in Figure 1) that emits a pair of particles toward two detectors (boxes on the left and right in Figure 1) in each trial of the experiment.
Alice and Bob randomly choose settings 1, 2 or 3 on their respective detectors in each trial of the experiment. When Alice and Bob's settings are the same in a given trial (case (a)), their outcomes are always the same, both red or both green. When Alice and Bob's settings are different in a given trial (case (b)), the outcomes are only the same one quarter of the time. So where's the mystery?
Well, let's try to account for case (a). Mermin said: "Why do the detectors always flash the same colors when the switches are in the same positions? Since the two detectors are unconnected, there is no way for one to 'know' that the switch on the other is set in the same position as its own."
This led him to introduce "instruction sets" to account for the behavior of the device when the detectors have the same settings (case (a)). In other words, the particles must agree, before they leave the source, on what outcomes they will render if measured in each of the three settings, just in case they are measured in the same setting. Concerning the use of instruction sets to account for case (a), Mermin said, "It cannot be proved that there is no other way, but I challenge the reader to suggest any."
These instruction sets constitute a "constructive effort" to account for the correlated case (a) outcomes. Sound familiar? Like the luminiferous ether, these instruction sets just don't work. It is easy to show that instruction sets will produce agreement in at least one third of all case (b) trials (the Bell inequality), far exceeding the one-quarter agreement actually produced by the device. So, instruction sets don't provide a causal mechanism to explain the predictions of quantum mechanics. And therein lies the mystery. Quantum mechanics provides a mathematical formalism that predicts the outcomes of case (a) and case (b), but it does not provide a constructive account of them. Just like the Lorentz transformations, we have a mathematical formalism that maps to the empirical phenomenon at hand, but does not provide a constructive account. This bothered Einstein.
Einstein's issue with quantum entanglement
In 1935, Einstein co-authored a famous paper, "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?" with Boris Podolsky and Nathan Rosen (known as the "EPR paper"). Essentially, Einstein did not believe quantum mechanics is complete because "for all its successes, [quantum mechanics] was stubbornly mute on the question of what is real." Without some constructive account of quantum entanglement otherwise, it seemed to Einstein that we needed some sort of instantaneous communication ("spooky actions at a distance") between the two particles to coordinate their outcomes when they are measured. One of the consequences of special relativity is that, if all reference frames are truly equal, you can't have instantaneous communication lest some observers see effects precede their causes. Einstein said:
"I cannot seriously believe in [the quantum theory] because it cannot be reconciled with the idea that physics should represent a reality in time and space, free from spooky actions at a distance."
It would seem that either quantum mechanics violates special relativity via "spooky actions at a distance" or quantum mechanics is incomplete, i.e., there is some "hidden causal mechanism" at work that quantum mechanics doesn't provide (much like the situation in special relativity). Since Einstein couldn't abide "spooky actions at a distance," he died believing quantum mechanics was incomplete.
What Einstein didn't know
The beautiful clarity of the Mermin device and its numerous experimental instantiations weren't available to Einstein, all being published long after his death. So perhaps he can't be faulted for missing the opportunity to employ his "universal formal principle" to yet another intractable mystery. That is, we are in a similar position today with quantum entanglement that physicists were confronting at the turn of the 20th century with time dilation and length contraction. What we showed in our paper in Science Reports is that the relativity principle is again responsible for the mystery.
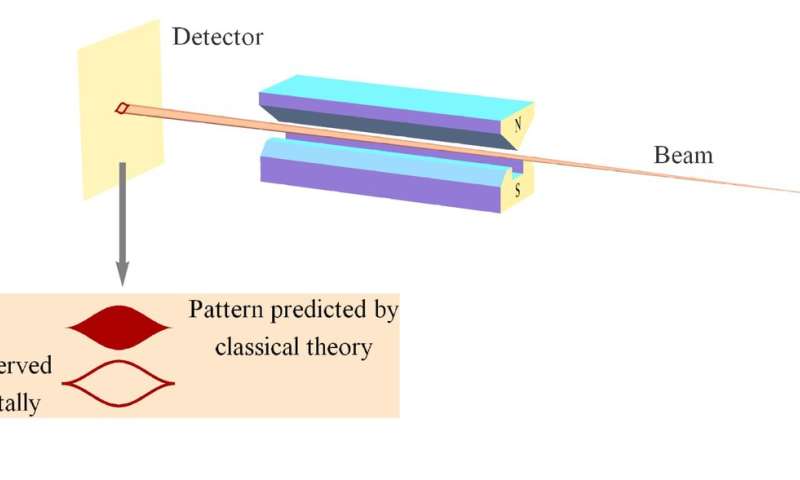
As Steven Weinberg points out, measuring spin angular momentum with Stern-Gerlach (SG) magnets constitutes the measurement of (plus or minus) "a universal constant of nature, Planck's constant h" (Figure 2). Therefore, the relativity principle requires that no matter how you orient the SG magnets to measure the spin angular momentum of the particles, you always obtain an up or down result, never a fraction of that amount. The red and green outcomes in the Mermin device represent these two possible outcomes. Just as one would expect to measure c + 20 miles per hour for the speed of the light pulses coming from the golf cart, one would expect (according to classical theory) to measure fractions of h at different SG magnet orientations (Figure 2).
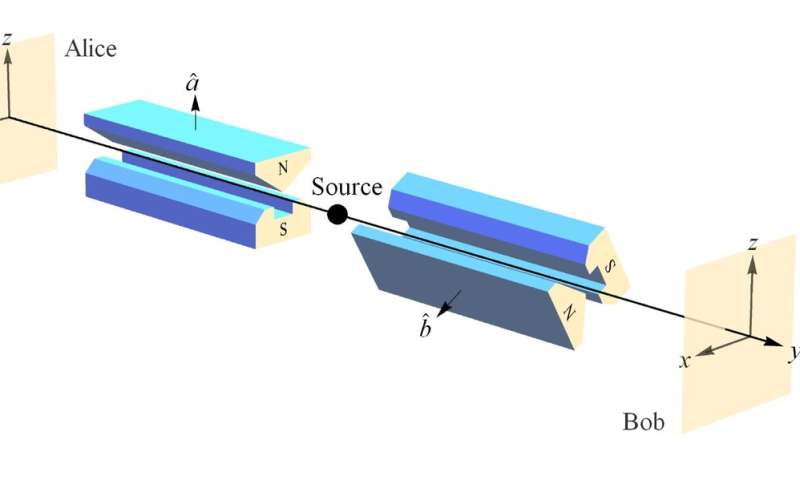
The behavior of the Mermin device is actually based on entangled spin measurements, i.e., measurements of the conserved spin angular momentum contained in the two particles (Figure 3). When the SG magnets are oriented the same way (case (a)), the outcomes are always the same due to conservation of spin angular momentum between the pair of particles. What we showed in our paper is that the mystery of quantum entanglement represented by the one-quarter case (b) agreement in the Mermin device results necessarily from the fact that neither Alice nor Bob can measure anything other than Planck's constant h, regardless of their SG magnet orientations relative to the source. In other words, in order to obtain the intuitive ("non-mysterious") conservation in case (b), Alice or Bob would have to measure something "between" red and green. But, that would mean the person who measured red or green was in a "preferred reference frame" having measured the "true" value of h.
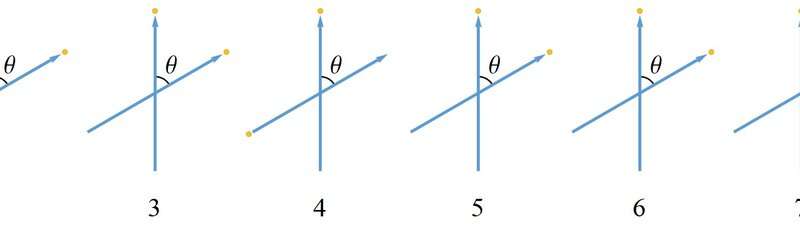
Instead, what happens in case (b) trials is that Bob's outcomes corresponding to Alice's outcomes for a particular setting correctly average to what one would expect for conservation of spin angular momentum (Figure 4). Of course, the situation is symmetric so that Bob can say it's Alice's outcomes that correctly average to what one would expect given his outcomes. Since no one can measure fractional outcomes, this "average-only" conservation is as complete a conservation of spin angular momentum as is possible.
When does principle explanation suffice?
So just as the mysteries of length contraction and time dilation follow from the relativity principle applied to the measurement of the speed of light c, the mystery of quantum entanglement follows from the relativity principle applied to the measurement of Planck's constant h. One-hundred fifteen years after Einstein published his theory of special relativity and 85 years after he published his famous EPR paper, we have one and the same principle explanation of these mysteries with no corresponding constructive accounts. Thus, we now know that quantum mechanics is as complete as special relativity given its adherence to the relativity principle. Einstein certainly missed a chance to rid us of "spooky actions at a distance" using his universal formal principle, but hindsight is … 2020.
This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.
More information:
W.M. Stuckey et al. Answering Mermin's challenge with conservation per no preferred reference frame, Scientific Reports (2020). DOI: 10.1038/s41598-020-72817-7 www.nature.com/articles/s41598-020-72817-7
Bio:
I earned a PhD in physics in 1987 with a thesis in general relativity (thesis advisor Louis Witten) and began teaching physics at Elizabethtown College in 1988. I read Mermin's paper in 1994, which inspired my work in foundations of physics. I have several publications in foundations of physics to include a book with Oxford UP, "Beyond the Dynamical Universe" (2018).