Bell's theorem refuted

May 20, 2021 by Eugen Muchowski
Bell's theorem refuted
Figure 1: Entangled photons are generated, for example, by parametric fluorescence with a BBO crystal. The ordinary photon beam has polarization 0° and the extraordinary photon beam comes with the polarization 90°. Each pho-ton leaves the source in a cone of light. Both cone shells intersect in beams 1 and 2, which are thus each a mixture of horizontally and vertically polarized photons in equal share. However, due to indistinguishability, their polarization is not defined and the photons are (by superposition) in singlet state 1/v2(|H1V2>-|V1H2>). The Hilbert space for the combined system is H12 = H1*H2. Normalized base vectors are |H1> and |V1> for system 1 at side 1 and |H2> and |V2> for system 2 at side 2. |H1> and |H2> correspond to the x-axis and |V1> and |V2> correspond to the y-axis. Credit: Eugen Muchowski

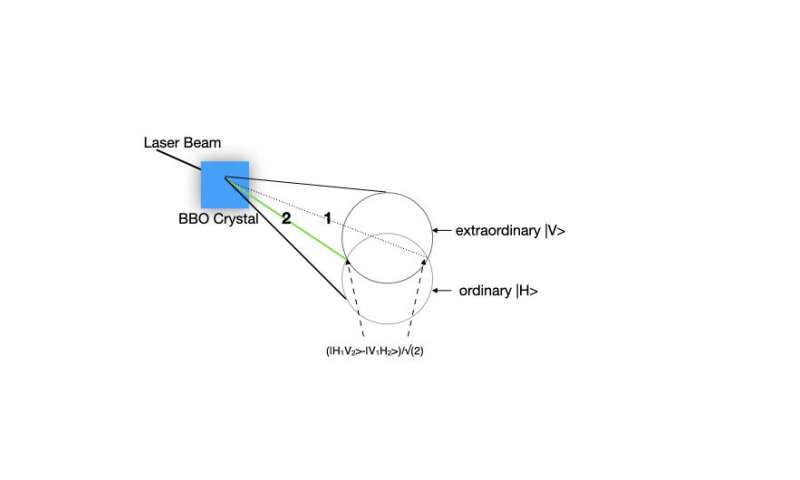
Einstein said that the wave function does not describe the physical state of a single object, but the possible states of an ensemble. He also said that quantum mechanics is not complete; there must be hidden variables. Not many believed him, but this was the starting point for me when I came in touch with Bell's theorem.

Bell's theorem states that the predictions of quantum theory (for measurements of spin on particles prepared in the singlet state, see figure 1) cannot be accounted for by any local theory. Bell stated this theorem in his own words: "In a theory in which parameters are added to quantum mechanics to determine the results of individual measurements, without changing the statistical predictions, there must be a mechanism whereby the setting of one measuring device can influence the reading of another instrument, however remote. Moreover, the signal involved must propagate instantaneously, so that such a theory could not be Lorentz invariant." In other words, nature is not local, as it cannot be described by local realistic models.

Bell's theorem can be refuted by presenting a contextual model which correctly predicts measurement results with entangled photons or spin ½ particles. Contextual models can have properties which are correlated with the setting of the measurement instruments. The reason for this is the indistinguishability of entangled particles. This also applies to any other theorem that claims that no local realistic model for quantum effects is possible if they fail to rule out contextual models. These include, for example, the theorems of CHSH, GHZ and Hardy.

For over 55 years, John Bell has misled the physicists community and made us believe that nature does show superluminal nonlocal interactions. This could have been proven experimentally, since the correlations of quantum physics violate Bell's inequality. But so far, nobody has found the slightest hint of how those nonlocal interactions work. Now we know that the assumption of spooky action at a distance, as Einstein called it, is unfounded; the correlations can be explained locally.

This also makes it clear that particles cannot be in different incompatible spin states at the same time. If that were the case, nonlocal interactions would have to occur with entangled particles because the measurement of the spin on one particle means that the opposite spin is measured on the other particle, regardless of the distance. As a consequence, the concept of a quantum computer also comes into question, as it relies upon the assumption that a quantum system bears simultaneous information about two mutually exclusive outcomes. As this assumption is no longer tenable, the diversity of the solution of a quantum computer is considerably restricted.

The paper, "On a contextual model refuting Bell's theorem," has now been published by the journal Europhysics Letters (EPL).

This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.

More information: Eugen Muchowski, On a contextual model refuting Bell's theorem, EPL (Europhysics Letters) (2021). DOI: 10.1209/0295-5075/134/10004

Researcher's bio:
Diploma in theoretical physics at the University of Karlsruhe, Germany, Doctoral degree in Chemical Engineering
PostDoc at the UC, Berkeley , CA, USA
Professional career in the industry, now retired

63 shares
Citation: Bell's theorem refuted (2021, May 20) retrieved 8 November 2024 from https://sciencex.com/news/2021-05-bell-theorem-refuted.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no part may be reproduced without the written permission. The content is provided for information purposes only.
Back to list