Quantum entanglement is explained in classic terms

In many quantum measurement experiments and thought experiments, measurement results appear that do not seem to have classic explanations. As example: In quantum particle spin experiments, entangled particles appear to interact instantly across distances; and in interferometer experiments, one measurement result appears to be split over two paths. Currently, these measurement phenomena are treated as unique to quantum mechanics and not understandable in classic physics. Recognizing calibration in theory explains and resolves all the differences that appear to occur between classic and quantum measurements.

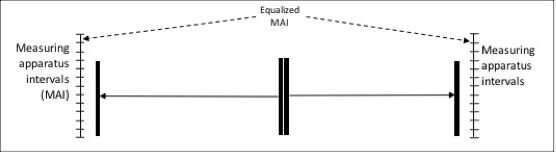
In the figure above, when the two vertical black bars in the center are moved to two measuring apparatuses and measured, a comparison of the two measurement results is equal only when both vertical bars are equal and all the measuring apparatus intervals (MAI) are equalized. This comparison of two measurement results, similar in form to particle spin experiments, requires MAI equalization, defined below as calibration in theory. When MAI equalization is not recognized in a measurement process, "spooky action at a distance" is seen instead.

This problem emerges from J. C. Maxwell's fundamental definition of a quantity with two independent factors: a numerical value and a "known quantity ... which is taken as a standard of reference" (e.g., gram, second, meter, etc.) In the quantity "3 grams," 3 is the numerical value and a gram (or a smaller or larger multiple of a gram) is the known quantity Maxwell defines as a unit.

A known gram, which is previously established, functions correctly in metrology based upon previous history, but not in a formal development based upon axioms. A comparison (ratio) of two quantities (one may be a reference) creates a measurement result. As the figure above demonstrates, the very first comparison between the measurement results of two measuring apparatuses, in theory or practice, is only possible when each MAI is equalized.

Calibration in theory, as defined here, is the initial equalization (within a tolerance) of each MAI. A standard of reference may be used to equalize each MAI and establish a measurement result, but a reference is only required when there is no other comparison. Applying calibration in theory maintains the two-factor quantity, but changes each unit to an MAI (a unit is known, an MAI must be equalized), compares each MAI to the others (or all the MAI to a reference), makes corrections (within a tolerance) to each MAI and sums the numerical value of all the corrected MAI to produce a measurement result.

Metrology defines calibration in practice (which might be termed re-calibration, as the units are previously known). In metrology, the numerical value of a measurement result is adjusted to compensate for unit variation. This is a successful practical approach which determines a mean MAI with a tolerance, but does not equalize each MAI.

Recognizing calibration in theory does not change the current approaches to quantum computing. It does identify that entanglement is not related to a superposition. Therefore, calibration-in-theory does not relate to wave/particle phenomena or the double-slit experiments. However, the transformation of a superposition of numerical values into a measurement result occurs when the units of a superposition become corrected MAI.

Check out the just published paper, "Measurement Unification," which explains the differences that appear in quantum particle spin experiments, quantum teleportation experiments, Mermin's device experiments, Mach-Zehnder matter-wave interferometer experiments, as well as Schrödinger's Cat thought experiment.

This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.