Structure of 3He: Small A nuclei are key to the nuclear force holding the atomic nucleus together
Findings in nuclear physics theory have received several Nobel Prizes (1975-nucleus vibrations and rotations, 1963-nuclear shell model, 1949-meson exchange model of nuclear forces). Despite these awards, the structure of the atomic nucleus continues to mystify; how did we get into this position? The critical branching point in the understanding of nuclear forces is April, 1936, with the publication in the Reviews of Modern Physics by Bethe and Bacher (https:/doi.org/10.1103/RevModPhys.8.82) of the then-known qualitative arguments of nuclear forces. Their key section: saturation of nuclear forces.
In contrast to electromagnetism, which allows charged particles in a plasma to interact with all other charged particles, the saturation property of nuclear forces means that the interaction energy only increases linearly with the number of nucleons present and not quadratic. Bacher and Bethe concluded that the nuclear force is analogous to chemical homopolar binding, which occurs in hydrogen's H2 molecule. Saturation is due to the exchange of electrons (Fermion exchange) since the finite number of electrons available sets the upper limit in covalent electron binding. In contrast, the electromagnetic plasma exchanges bosons (photons), which have no restrictions in number.
Now, the stage was set for the greatest prediction ever made in the history of science: Bethe and Bacher predicted in 1936 that the neutron and proton are not elementary, that they are composed of more elementary particles, fermions, which, being exchanged between nucleons which have overlapping nucleon wavefunctions, leads to the binding energy holding the atomic nucleus together. But they don't do it! Many years later, I wrote Professor Bethe asking why he did not predict the existence of quarks, based on his deep understanding of the nuclear force. He replied, "It would have been too great a leap to make." Tragically, the omission had consequences that led to many decades of divergent work attempting to explain the nuclear forces with bosons and phenomenological nuclear models.
Experimental physics can reveal the structure of the atomic nucleus by means of high-energy elastic electron scattering, totally analogous to X-rays scattering off molecules, revealing the molecules' 3D structure. In both cases, the non-coherent projectile beam leads to diffraction patterns. However, there is an important detail difference. The Born-Oppenheimer approximation for molecules (separating nuclear motion from electronic motion) means that the Pauli Exclusion Principle for the many-body electron wavefunction reduces to a simple formula, since the exchange integrals can be neglected. For example, it was easy to see (if you are good at Fourier transforms) that the X-ray diffraction pattern off crystalline DNA is a double helix. In contrast, the atomic nucleus is a true many-body system of overlapping nucleon wavefunctions, and the Pauli Exclusion Principle for nucleons creates very complicated quantum mechanical wavefunctions.
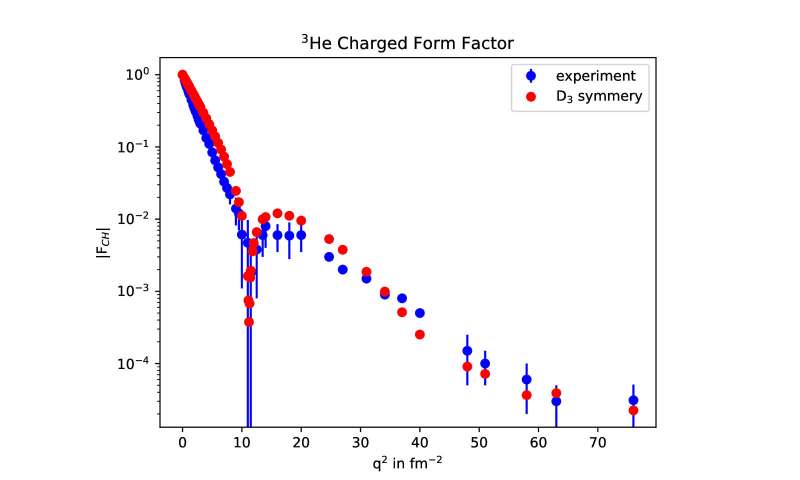
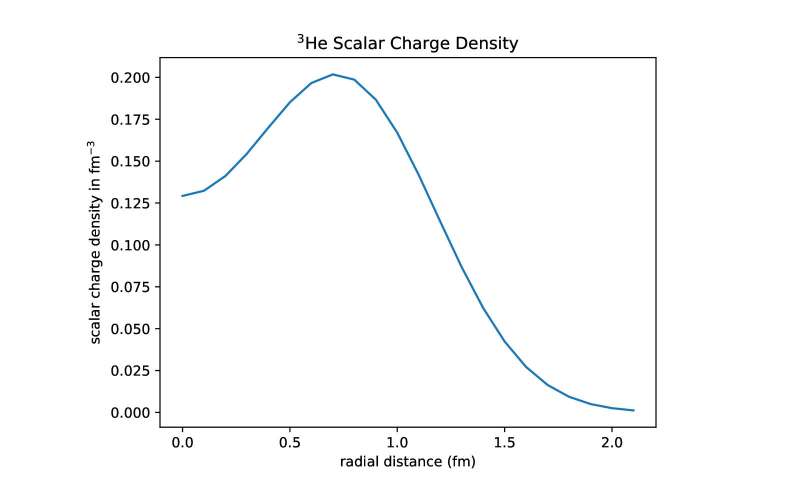
The diffraction pattern off the a-particle (A = 4 = 2 neutrons + 2 protons) revealed complexity that defied analytical understanding. The nuclear shell model predicted the a-particle to be a sphere, the first closed shell, but it failed to explain the experimental data. Finally, using advanced group theory techniques with projection operators, the a-particle was shown to be a three-base pyramid (https:doi.org/10.1007/BF01355593). However, the diffraction pattern off of 3He (A = 3) remained unexplained until now. In Figure 1, the electron scattering data (charged form factor FCH as a function of squared-momentum transfer) for 3He is shown along with the solution to its structure, where the solution used the one-photon scattering approximation and the neglect of the neutron. The 3He solution is an equilateral triangle with dihedral symmetry. If we take the solution's quantum mechanical charge density operator and integrate it over the unit sphere, we get the solution for the scalar charge, shown in Figure 2. It reveals that 3He has a hole in its center.
Finally, the atomic nucleus reveals its secret: The nucleons are held together by two-body, three-body and four-body quark exchange forces. The two-body force has scalar, spin, tensor and spin-orbit effective nucleon interactions. The three-body forces are scalar and spin-dependent, while the four-body is scalar in its interaction. The excitations are either coherent, keeping the bonds intact and leading to vibrations and rotations of the atomic nucleus (resulting in collective motion), or incoherent excitations, which break the bonds; quark exchange explains why A = 5 nuclei do not exist. The bonds' spin-dependence leads to generally simple odd-A, even-A ground-state angular momentum assignments. The picture that appears is that we are facing a protein-folding problem, leading to point-group-symmetry, more complicated than actual biological proteins.
This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.
More information: Original Bethe & Bacher Review: H. A. Bethe et al, Nuclear Physics A. Stationary States of Nuclei, Reviews of Modern Physics (2002). DOI: 10.1103/RevModPhys.8.82
Original Alpha Particle Solution: P. D. Morley et al, On the structure of the alpha particle, Zeitschrift for Physik A Atomic Nuclei (2005). DOI: 10.1007/BF01355593
New 3He solution being reported: P. D. Morley, Structure of 3He, Scientific Reports (2021). DOI: 10.1038/s41598-021-98416-8
Dr. Peter Morley is a theoretical physicist that does research in astrophysics, nuclear physics and elementary particle physics. A list of his papers can be found here: inspirehep.net/authors/996788