"The Music of the Spheres": We think that we've found its equation

Pythagoras (569-490 BC) established that the octave (the ratio 1:2 of a string's length) was the fundamental musical interval and saw it as a sign that nature itself, including the planetary orbits ("the spheres"), is governed by numerical ratios. "There is geometry in the humming of the strings and there is music in the spacing of the spheres," he concluded. In "Mysterium Cosmographycum and Harmonices Mundi," Kepler (1571-1630) further developed Pythagoras' ideas and suggested that the planets of the solar system are spaced according to specific geometries and produce tones as they orbit the sun.

Today, it is well established that several orbital systems are characterized by harmonic resonances, which are usually the result of self-organizing gravitational or tidal processes yielding long-term stable orbits. For example, in our solar system, five periods of Jupiter approximately correspond to two periods of Saturn; 13 orbital periods of Venus approximately correspond to eight periods of the Earth, and so on. Also some exoplanetary systems, such as the Trappist-1 solar system, exhibit remarkable synchronization between their planetary orbits. However, no other orbital system like ours has been discovered, and nobody has so far been able to determine whether the architecture of the solar system corresponds to a precise mathematical order. Attempts have been made to describe the spacing of the planetary orbits; the most famous model is the Titius–Bode law of planetary distances, which, however, has serious shortcomings.

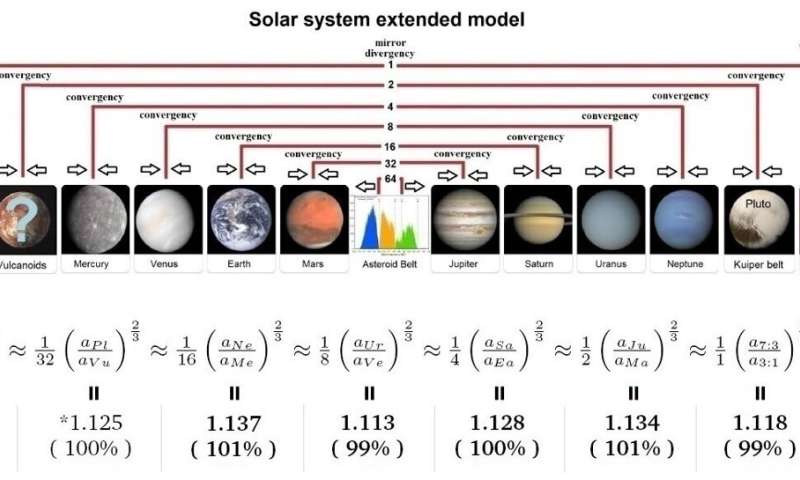
We discovered an equation that relates the spacing of the orbits of the solar system. It is depicted in Figure 1 and emphasizes both mirror and scaling features. We obtained it by using mathematical metrics derived from the popular 12-tone music tuning systems, which divides the octave into 12 notes.

We focused on the most distinctive feature of the solar system: its mirror-reflection architecture with respect to the asteroid belt located between Mars and Jupiter. This feature was first studied by Geddes and King-Hele in 1983.

The solar system is composed of four inner terrestrial planets (Mercury, Venus, Earth and Mars) and four outer gas giant planets (Jupiter, Saturn, Uranus and Neptune) separated precisely by the asteroid belt. Four mirrored planetary pairs can be readily identified using the asteroid belt as the mirror point: Jupiter-Mars, Saturn-Earth, Uranus-Venus, and Neptune-Mercury.

We discovered that for each pair, when the ratio between the orbital radii of the two planets is raised to the power of 2/3 (which should not be confused with the exponent used in Kepler's third law that is 3/2) it is twice as large as the same ratio derived from the internally adjacent mirrored planetary pair. For example, given the orbital semi-major axes a₂ < a₁ < asteroids < b₁ < b₂, we have (b₂/a₂)^2/3 = 2(b₁/a₁)^2/3. In this way, a scaling relation, which is characterized by the sequence of the powers of 2 (1, 2, 4, 8, 16, etc.), emerges among contiguous mirror-symmetric orbital planetary pairs.

We also found that the same relation relates the orbital radii that correspond to the two main Kirkwood asteroid gaps that are generated by the 3:1 and 7:3 resonances of Jupiter, which indicates that the planetary self-organization of our solar system is due to Jupiter. Finally, we can postulate two additional pairs of gravitational rings that complete the structure of the solar disk: They include, on the outer side, the Kuiper Belt and the scattered disk, respectively, and, on the inner side toward the sun, the hypothesized Vulcanoid asteroid belt and the empty region surrounding the sun.

By taking a as the length of the semi-major axis of an orbit, the found scaling equation linking together all planetary pairs is depicted in Figure 1. For each ratio, the figure also shows the value (val.) and its accuracy (acc.) relative to the ratio 9/8 = 1.125. We found that each planetary-pair ratio differs from the ratio 9/8 by no more than 1 percent, which suggests that the found equation is quite robust. The proposed equation appears "elegant" and is clearly suggestive of a planetary "order," that is, a "kosmos," as Pythagoras would have called it.

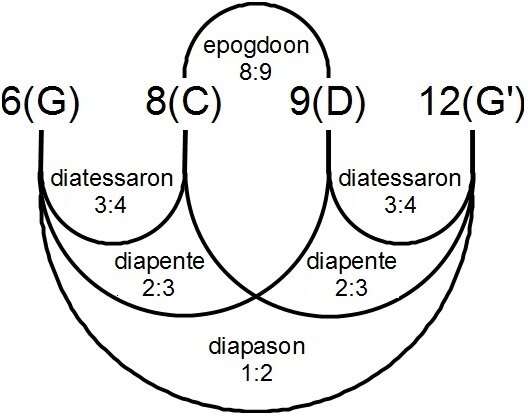
The fundamental ratio of the planetary scale is 9:8. This ratio is important in the history of mathematics and music because it is the Pythagorean epogdoon, which is displayed by Raphael in a famous detail of his masterpiece "The School of Athens."

In music, the epogdoon is the difference between the Perfect Fifth and the Perfect Fourth, which is a whole-tone; for example, the interval from C to D. Figure 2 summarizes the Pythagorean music theory with a diagram showing the relations between the epogdoon, diatessaron, diapente, and diapason, which correspond to the Major Second (9/8), Perfect Fourth (4/3), Perfect Fifth (3/2) and Octave (2/1), respectively.

The musical interpretation of our model and its robustness in predicting the relative spacing among the planets of the solar system is further detailed in our published paper. For example, the scaling involving consecutive powers of 2 musically corresponds to tones on subsequent octaves. We also found that by using the same metrics, the ratios of the orbital radii of neighboring planetary pairs elevated to the 2/3 power correspond to four musical "consonances" having frequency ratios of 5/4 (Major Third), 4/3 (Perfect Fourth), 3/2 (Perfect Fifth) and 8/5 (Minor Sixth). The probability of obtaining this result randomly has a p < 0.001.

Musical consonances are "pleasing" tones that harmoniously interrelate when sounded together, which further suggests that the orbits of the planets of the solar system could form a gravitationally optimized and coordinated structure mimicking musical harmony. On the contrary, dissonant ratios were found when the Kirkwood asteroid gaps, the scattered disc (characterized by Eris), and the region closest to the sun were considered: Indeed, these are gravitationally divergent regions.

Thus, the discovered equation (depicted in Figure 1) appears to fully characterize the solar system and supports the idea that a harmony described by typical music tone ratios characterizes the solar system, as Pythagoras and Kepler conjectured. It performs better than any other model proposed in the literature.

Our empirical finding—which involves a metric that uses orbital radii raised to the power of 2/3—suggests that the planetary organization of our solar system could be peculiar and based on more complex and unknown dynamical structures that require further investigation.

This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.

More information: Michael J. Bank et al, Scaling, Mirror Symmetries and Musical Consonances Among the Distances of the Planets of the Solar System, Frontiers in Astronomy and Space Sciences (2022). DOI: 10.3389/fspas.2021.758184

Nicola Scafetta has a Ph.D. in Physics from the University of North Texas and was a researcher at Duke University. He is currently a professor in Physics at the University of Naples Federico II, Italy. His expertise is in the Physics of Complex Systems and, in particular, in the fields of solar, planetary, and climate physics. Michael J. Bank is a musician associated with the Danbury Music Centre.