Quantum information theorists produce new 'understanding' of quantum mechanics

Richard Feynman famously said, "I think I can safely say that nobody understands quantum mechanics." Since Feynman won a Nobel Prize in physics for his work in quantum theory, he certainly understood how to use it. Indeed, quantum mechanics (QM) "has survived all tests" and "we all know how to use it and apply it to problems," yet Murray Gell-Mann (who also won a Nobel Prize for his work in quantum theory) agreed with Feynman, saying, "we have learned to live with the fact that nobody can understand it."

What they meant was that the fundamental principles upon which QM is built are mathematically abstract, so they don't "make sense" in and of themselves. Since physics is a reductive explanatory discipline, the fundamental principles or axioms of a theory are not themselves explicable via that theory. So if the theory is to be "understood," those fundamental principles or axioms must "make sense" in and of themselves. In response to this state of affairs, quantum information theorists have reorganized the mathematical structure of QM in an attempt to discover information-theoretic axioms at the foundation of QM that "make sense," so that QM can be "understood." What they have discovered may surprise you.

Desideratum of QM reconstructions

Lucien Hardy is generally credited with producing the first of these "axiomatic reconstructions of QM based on information-theoretic principles" in his 2001 paper, "Quantum Theory from Five Reasonable Axioms." Since then, many more such reconstructions have been produced, and there is excitement in the quantum information community about these information-theoretic reconstructions of QM. For example, Markus Müller said:

Can quantum theory be derived from simple principles, in a similar way as the Lorentz transformations can be derived from the relativity principle and the constancy of the speed of light? The exciting answer is "yes," and our group has made substantial contributions to this research goal.

As you can see from his statement, the goal is to find axioms for QM that "make sense" like Einstein's postulates of special relativity (SR).

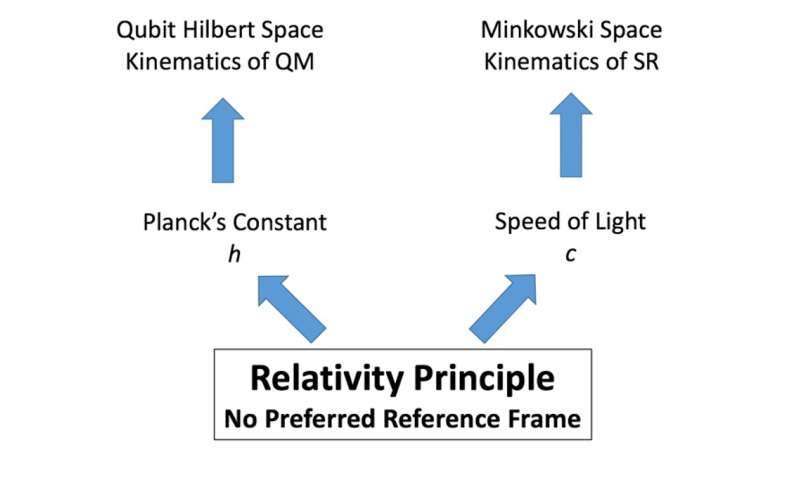
To remind you, the first of Einstein's postulates of SR is the relativity principle: "The laws of physics must be the same in all inertial reference frames," aka "no preferred reference frame" (NPRF). The second postulate (aka "light postulate") is that "Everyone measures the same speed of light, c, regardless of their motion relative to the source," and it arguably follows from NPRF. That is, Maxwell's equations of electromagnetism, which are laws of physics, predict a value for c, so NPRF implies that everyone must measure that same value. The combination of the relativity principle and light postulate ("NPRF + c" for short) leads to the kinematic structure at the foundation of SR called Minkowski space with its Lorentz transformations between inertial reference frames. Thus, Chris Fuchs says that it would be "a worthwhile exercise to try to reduce the mathematical structure of quantum mechanics to some crisp physical statements" like those of SR.

What quantum information theorists discovered

In Hardy's original 2001 paper, he noted that by deleting the single word "continuous" from his fifth axiom, "there exists continuous reversible transformations between pure states," his five "reasonable" axioms produce classical probability theory instead of quantum probability theory. Many quantum information theorists have since acknowledged the importance of "continuous reversibility" in their axiomatic reconstructions of QM. For example, Adam Koberninski & Markus Müller said: "We suggest that (continuous) reversibility may be the postulate which comes closest to being a candidate for a glimpse on the genuinely physical kernel of 'quantum reality.'"

Caslav Brukner & Anton Zeilinger capture it up nicely in their fundamental information-theoretic principle of Information Invariance & Continuity:

The total information of one bit is invariant under a continuous change between different complete sets of mutually complementary measurements.

As you can see, quantum information-theoretic principles are very general statements. This is intentional, as quantum information theorists are looking for principles that can be applied to the widest possible array of physical instantiations. While this generality makes them very powerful explanatory principles, the unfortunate corollary is that information-theoretic principles are not quite as transparent as Einstein's postulates of SR. Thus, some of us working in foundations of quantum mechanics, but not in quantum information theory per se, have not fully appreciated the foundational implications of principles like Information Invariance & Continuity. Consequently, not everyone in foundations of quantum mechanics finds information-theoretic principles helpful in "understanding" QM.

Highlighting an important implication

In order to help others like ourselves (physicist W.M. Stuckey, mathematician Timothy McDevitt, and philosopher Michael Silberstein) appreciate the explanatory power of these QM reconstructions, we published "No Preferred Reference Frame at the Foundation of Quantum Mechanics." In this paper, we explain how the fundamental principle of Information Invariance & Continuity actually entails the relativity principle applied to the invariant measurement of Planck's constant h, in exact analogy to NPRF + c for SR. We did this by choosing an apropos physical instantiation, i.e., the Stern-Gerlach (SG) measurement of spin.

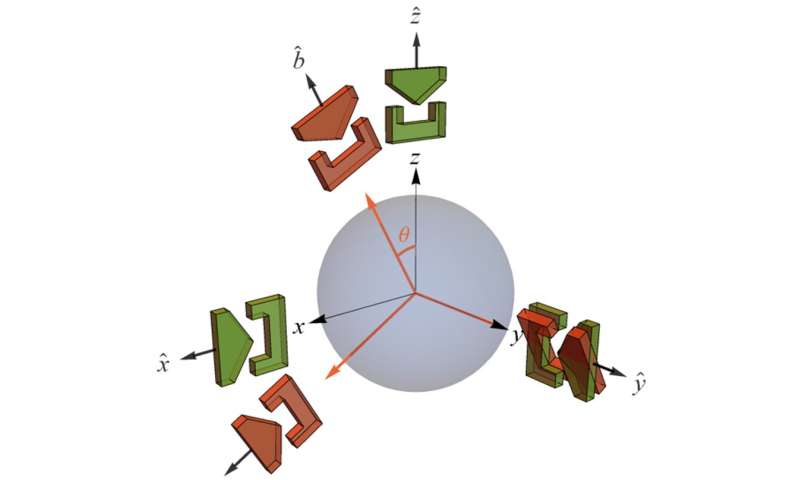
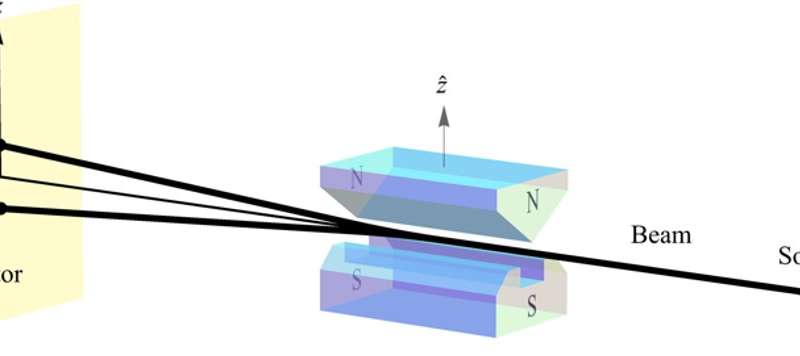
Figure 1 is a schematic showing the SG spin measurement of a beam of electrons, e.g., via the valence electron of a silver atom in the original experiment. The SG magnets are aligned along the z axis and two spin measurement outcomes obtain, i.e., up (+1) and down (-1) relative to z-hat. Thinking of each electron as possessing a magnetic moment oriented randomly in space, we would classically expect such a measurement to produce all possible deflections of the electron beam. [Note: The SG magnetic field near the N pole is stronger than that at the S pole, so its effect on the electrons dominates.]

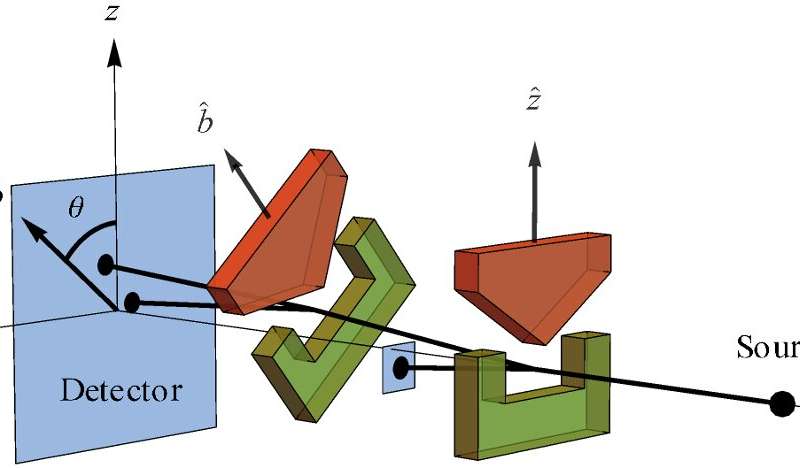
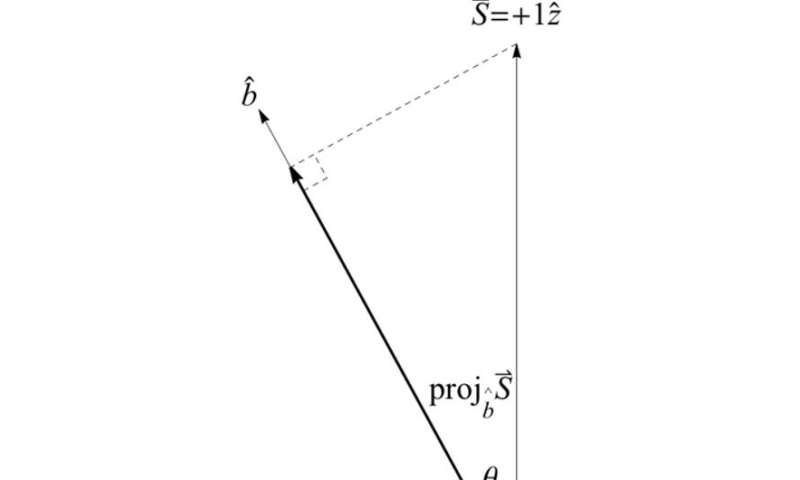
Since, as shown in Figure 1, the measurement only produces two deflections, up and down, we might then believe that for some strange reason, the source is only producing electrons with magnetic moments aligned or anti-aligned along z-hat. In that case, if we do a subsequent spin measurement of the spin up (S = +1 z-hat) beam along a new direction b-hat rotated by theta relative to z-hat (Figure 2), we simply expect a reduced beam deflection of cos(theta) along b-hat (Figure 3). But mysteriously, we continue to see only up and down deflections along direction b-hat, just as we saw along z-hat (Figure 2).

As Steven Weinberg points out, these SG spin measurements constitute the measurement of (plus or minus) "a universal constant of nature, Planck's constant h" (h divided by 4 pi to be exact). Thus, someone could have used Planck's discovery of this universal constant of nature via his blackbody radiation equation (a law of physics), along with the relativity principle, to predict this mysterious property of electron spin before the Stern-Gerlach's experiment. In the case of measurements of c, the different inertial reference frames are related by different relative velocities. In the case of SG measurements of h, the different inertial reference frames are related by different relative orientations in space (Figure 4). "Boosts" and "spatial rotations" are valid transformations between inertial reference frames in both Galilean and Lorentz transformations.

All of this follows as a particular example of the principle of Information Invariance & Continuity. The bit of information (measurement outcome of plus or minus h, Figure 1) is conserved (must be the same, Figure 2) under a continuous change between different complete sets of mutually complementary [spin] measurements (between different inertial reference frames related by spatial rotations, Figure 4). And, requiring that the distribution of outcomes average to cos(theta) (Figure 3) gives the distribution of spin measurement outcomes per the qubit Hilbert space structure at the foundation of the axiomatic reconstructions of QM.

Thus, quantum information theorists have shown that NPRF + h leads to the kinematic structure at the foundation of QM called Hilbert space, in exact analogy to NPRF + c leading to the kinematic structure at the foundation of SR called Minkowski space (Figure 5).

Surprising result?

If one conflates the relativity principle with the theory of relativity, it will seem impossible that the relativity principle resides at the foundation of non-relativistic quantum mechanics. But the relativity principle is not restricted to the laws of classical physics, it pertains to all physics. And that a theory harbors the relativity principle at its foundation does not imply that the theory is "relativistic." Newtonian mechanics with its Galilean transformations between inertial reference frames conforms to the relativity principle and Newtonian mechanics is certainly "non-relativistic." Thus, there is no reason a priori to reject this result as impossible.

Conclusion

Virtually all introductory physics textbooks introduce SR via NPRF + c, because NPRF + c "makes sense" to most physicists. Thus, one does not hear Nobel laureates in physics saying, "No one understands special relativity." Hopefully, NPRF + h will help physicists "make sense" of Information Invariance & Continuity at the foundation of axiomatic reconstructions of QM, and Nobel laureates in physics will no longer say, "No one understands quantum mechanics."

This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.

More information: William Stuckey et al, No Preferred Reference Frame at the Foundation of Quantum Mechanics, Entropy (2022). DOI: 10.3390/e24010012

Bio: William Stuckey earned a PhD in physics in 1987 with a thesis in general relativity (thesis advisor Louis Witten) and began teaching physics at Elizabethtown College in 1988. He has several publications on the foundations of physics to include a book with Oxford UP, "Beyond the Dynamical Universe" (2018), coauthored with Timothy McDevitt and Michael Silberstein.