Pooling strategies can reduce the cost of COVID-19 PCR tests, even at high prevalence
Large-scale testing and contact tracing play a fundamental role in the containment of COVID-19 outbreaks. The task is nevertheless rendered difficult by the existing limitations on test analysis facilities and trained personnel. Moreover, the cost associated with accurate RT-PCR tests and the shortage of required chemical reagents poses severe challenges in the implementation of a mass testing policy.
To address the problem, an emerging trend is to use pooling (or group testing) to reduce the test analysis time, effort and costs. Group testing was originally introduced by R. Dorfman in 1943, as a technique to efficiently test for syphilis World War II soldiers. Since then, group testing has been used successfully in biology and production chains to identify "defective" elements.
Recently, the use of group testing has been advocated to enable mass testing in the context of the ongoing COVID-19 pandemic, with experimental campaigns implemented is a few countries. Given the human and economical cost of the current outbreak, to improve the level of preparedness to future pandemic events, it is conceivable that, in the medium run, developed countries will work to establish centers (possibly, with a high degree of automation) capable of analyzing massive quantities of tests, partly thanks to advanced group testing methodologies.
How pooling works
Dorfman's original idea is to group the samples collected from different individuals of pools. The number of individuals participating in a pool is typically fixed to some low number (e.g., four or five) to mitigate so-called dilution effects. The approach consists of mixing the samples within each pool, and then to perform a test on each mixed pool (see Figure 2). If the test result is negative, all participants in the pool are declared as non-infected (Figure 2, left). On the contrary, we know that at least one participant in the pool is infected (Figure 2, right). To identify the infected sample, an individual test is carried out for each participant in the pool.
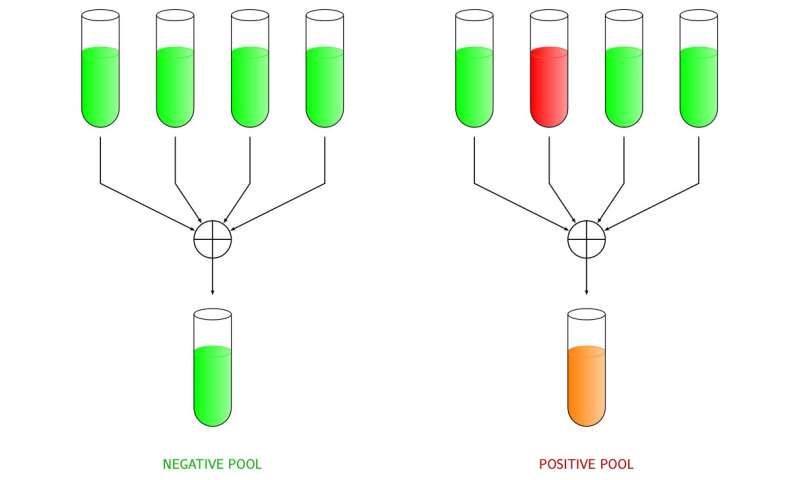
The advantage of this strategy becomes evident when the prevalence (i.e., the fraction of infected individuals) is small, as most of the pools will give a negative result, allowing a drastic reduction of the number of tests.
Pooling strategies
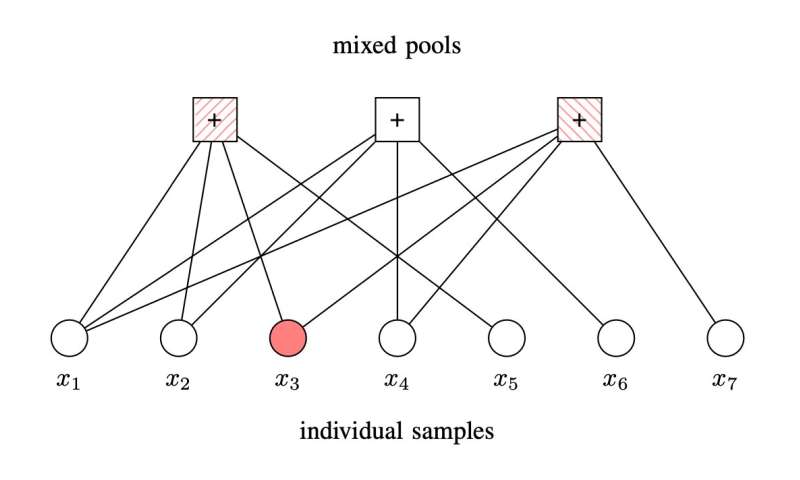
An example of a more complex pooling strategy is presented through the following example. Consider a population of seven individuals xi, with i ranging from one to seven. We create three pools of four individuals each, as summarized in Figure 3 by means of a graph, where circles denote the individuals, squares the pools, and edges relate individuals to pools. In the example, only the third individual is infected, yielding a positive test outcome for the first and the third pools.
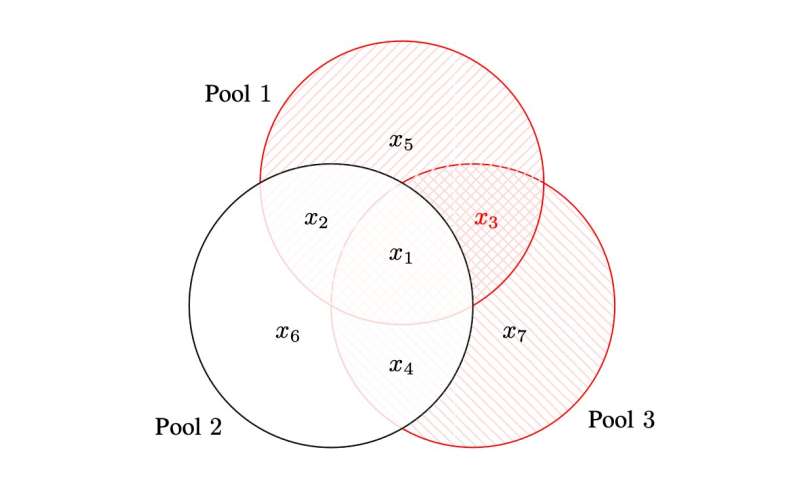
By observing that the second pool resulted negative, we infer that all its participating individuals are not infected. This leaves us with three possible infected members, i.e., x3, x5, and x7. At this point, we may decide to test each of them individually, or, in case of low prevalence, we may look for the smallest subset of labels among x3, x5, and x7 which, if positive, yields the observed outcome of the pool tests. If we follow the latter approach, we identify x3 as the unique infected element in the pool. The idea is summarized in Figure 4 through a Venn diagram. The result is obtained by running three tests, rather than seven individual tests, thus more than halving the required amount of tests.
We should observe that the procedure described in the example may not succeed in identifying the infected individuals when more than one are infected. As for the basic Dorfman scheme, the technique is suitable when the prevalence is sufficiently low.
A pooling strategy for COVID-19 PCR tests at high prevalence
At the peaks of the spread of SARS-CoV-2, it was common to hear news about tragically-high rates of positive PCR tests, well above the prevalence values for which simple, Dorfman-like pooling strategies yield tangible gains. To address this issue, we developed an approach to group testing that retains the simplicity of the simplest pooling techniques and that extends its applicability to the high prevalence regime.
The idea relies on two rounds of testing. In a first round, small pools (comprising, for instance, three or four individuals) are formed. The groups are formed by enforcing each individual to participate in two separate pools—with the additional condition of avoiding any two pools to share more than one individual. The definition of the pooling groups can be well summarized via complete graphs (i.e., graphs where there is an edge connecting every vertex pair, see Figure 5) where each individual corresponds to an edge, and each pool to a vertex.
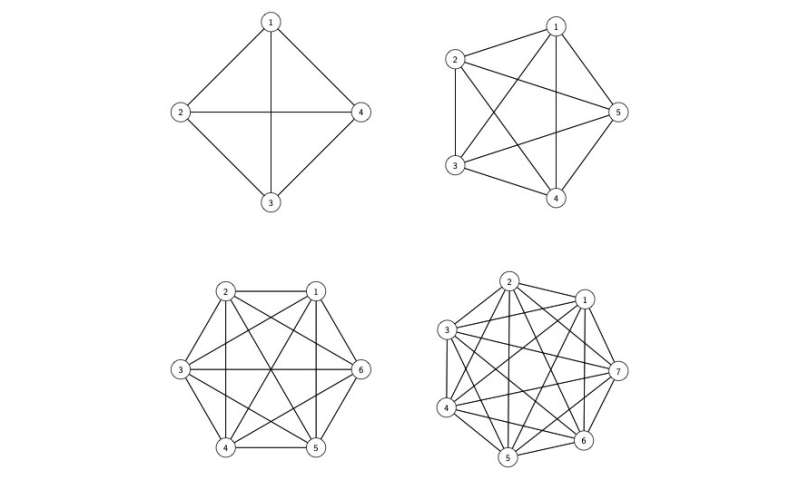
After the first round, three conditions can be verified. A possibility is that no infected samples are detected. Alternatively either a single infected sample is identified, or the presence of multiple infected samples is detected. Obviously, in the first case no further action is required: we can declare all pools participants as non infected. In the second case, we can immediately pinpoint the infected individual, without the need of additional tests. In the third case, we can call individual tests to find the infected individuals.
This approach works remarkably well even in the high prevalence regime. Dilution effects are mitigated by the small size of the pools. Notably, we maximize the fraction of samples that are classified positive/negative in the first round. With a prevalence of 5% and pools made by six individuals, by running 100 tests, we can classify 242 individuals, out of which 92% are classified in the first round—and the remaining 8% requiring a second individual test. In our study published in Scientific Reports, we remark that with an optimized Dorfman's scheme, we can test 229 individuals with 100 tests, with a second round involving 18.5% of the individuals.
Considering the current expenses for COVID-19 tests, for example several million dollars per day in Italy assuming on average 200,000 tests/day with a cost of 30 to 60 euros each, these techniques can bring considerable money savings or, with the same money, can allow to perform larger test campaigns. Moreover, the technique is general and can be applied to other diagnosis tests, even beyond the medical area.
This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.
More information:
Marco Chiani et al, Identification-detection group testing protocols for COVID-19 at high prevalence, Scientific Reports (2022). DOI: 10.1038/s41598-022-07205-4
Marco Chiani and Enrico Paolini are with DEI, University of Bologna, Bologna, Italy
www.unibo.it/sitoweb/marco.chiani/en
www.unibo.it/sitoweb/e.paolini/cv-en
Gianluigi Liva is with the Institute of Communications and Navigation, German Aerospace Center (DLR), Wessling, Germany
www.wirelesscoding.org/